Area Of A Kite Formula

Surface area of a Kite

Kite Surface area Formula

A kite is a quadrilateral with two pairs of equal-length sides. The equal length sides are ever reverse each other. There are ii simple formulas for finding the area of a kite. They are given as:

1.) A = d_oned_ii/ii
2.) A = absin(c)

WhereA is the surface area, d₁ is the long diagonal, d_ii is the short diagonal, a is the short side, b is the long side, and c is the angle between short and long sides.

The diagonals method can be considered the simpler of the 2 considering it only involves 2 basic length values. The trigonometry method requires us to know the bending between unequal sides. See the epitome below for how these dimensions within a kite are notated.

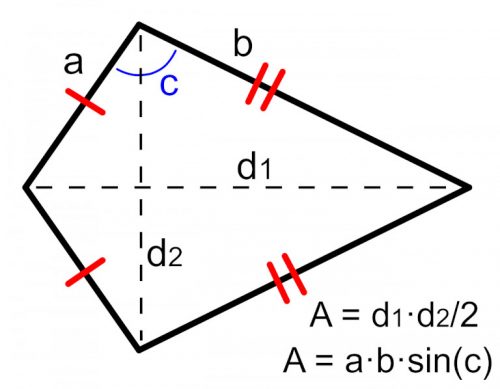
Formula 1: Using the Diagonals to Detect Area

If we know the diagonals of a kite, nosotros can employ the diagonals formula to discover area. The formula is given as:

A = d₁d_ii/2

Where d₁ is the long diagonal and d₂ is the short diagonal.

Here'south an example of using this formula for a kite with a long diagonal length of iv and curt diagonal length of 2:
A = d_aned₂/ii
A = (4)(2)/2 = 8/2 = iv

Formula two: Using Trigonometry to Find Area

If we know the side lengths and angle betwixt unequal sides, nosotros can use trigonometry to observe surface area of a kite. The formula for this is given equally:

A = absin(c)

Where a is the length of the brusque side, b is the length of the long side, and c is the internal bending between those ii sides.

Here's an example of using this formula for a kite with a side a length of 4, a side b length of 7, and an internal angle c value of 100 degrees.
A = absin(c)
A = (4)(7)sin(100°) = (28)(0.9848) = 27.574