Finding Multiples Of A Number

Introduction

Multiplication and sectionalization are ii of the important operations in mathematics. We can multiply a number by any number. Similarly, a number tin can be divided by whatever number. Two of import terms that are related to the multiplication and division of numbers are factors and multiples. The understanding of one of these is incomplete without studying the other. Therefore, earlier nosotros move ahead and larn most multiples let us know what we hateful by factors of a number.

What are Factors?

A factor of a number is an verbal divisor of that number. In other words, a factor of a number is that number that completely divides the number without leaving a remainder. For instance, each of the numbers, one, two, 3, 4, vi and 12 is a factor of 12. Nonetheless, none of the numbers 5, 7, 8, 9, x and 11 is a factor of 12.

What is a multiple?

A multiple of a whole number is the product of the number and whatever counting number. If we multiply 3 by one, ii , 3 , 4, 5 , six ….. we get

3 x ane = 3

three x two = 6

iii x 3 = ix

3 x 4 = 12

3 10 5 = 15

3 10 6 = eighteen etc.

Thus iii, six , 9 , 12 , 15 , xviii and and so on are the multiples of 3.

Permit usa now look at the properties that are satisfied by the multiples.

Properties of Multiples

Every multiple of a number is greater than or equal to that number. For example, the multiples of v are 5, 10, 15, 20, 25, ……. . In fact, the multiples of a number are obtained past multiplying the number past 1, ii, three, iv, 5, 6 …. and then on. Therefore, the smallest multiple of a number is the number itself. Hence, every multiple of a number is greater than or equal to the number itself.
The smallest multiple of a number is the number itself. Since every number can be multiplied by i to get the same number, therefore, every number is a multiple of itself.
The number of multiples of a given number is infinite. For example, the multiples of 7 are 7, 14, 21, 28, 35 and and then on. We can see that this is a never ending list. Hence, the number of multiples of a given number is infinite.
All multiples of 2 are fifty-fifty numbers. We know that 2, iv, 6, 8, 10, 12 and so on are the multiples of ii. As well, all these numbers two, iv, 6, 8, 10, 12 ….. are fifty-fifty numbers. Hence, all multiples of two are even numbers.

Allow united states of america understand multiples through an case.

Example

Write outset five multiples of 17.

Solution

In lodge to obtain tehf irst five numbers of 17, nosotros will multiply it by 1, 2, 3, and 5. We will get –

17 10 1 = 17

17 x 2 = 34

17 x iii = 51

17 ten 4 = 68

17 10 v = 85

Hence, the first v multiples of 17 are 17, 34, 51, 68 and 85.

Mutual Multiples of Numbers

We have now understood what we mean by multiples of numbers. Now, if we look at two or more than numbers simultaneously, nosotros can obtain some common multiples of those numbers. For instance, we if accept two numbers 4 and 6, we tin can hands say that 12 is a common multiple of both four and half dozen as 4 x 3 = 12 and half-dozen x2 = 12. This means that ii or more numbers tin accept common multiples. Those multiples which are common among the multiples of ii or more numbers are known equally common multiples of those numbers.

Let the states understand this using an example –

Case

List 3 common multiples of 3, 4 and 9

Solution

We accept been given three numbers 3, 4 and 9 and nosotros need to detect common multiples of these iii numbers.

Let us first write the multiples of the given numbers separately. We will take,

Multiples of 3 are 3, 6, 9, 12, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, xc, 93, 96, 99, 102, 105, 108, 111 ……….

Multiples of iv are 4, viii, 12, 16, twenty, 24, 28, 32, 36, 40, 44, 48, 52, 56, sixty, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100, 104, 108, 112 ……..

Multiples of nine are 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117 …….

From the higher up multiples of 3, four and nine we can run across that the common multiples of 3, 4 and half-dozen are 36, 72 and 108.

Hence, common multiples of three, 4 and 6 are 36, 72 and 108.

From above we tin see that though in that location is no finish to the list of multiples, at that place is always the beginning multiple of a number or grouping of numbers. Therefore, we cannot define the largest multiple of a number or a group of numbers but nosotros can e'er listing out the first multiple of a number. In the case of a group of numbers, this first multiple is likewise the least common multiple of these numbers.

Let us find out what we mean by the least common multiple of numbers.

To the lowest degree Common Multiple ( L C Grand )

If a number is a multiple of two or more numbers, it is called a common multiple of the numbers. For example, we know that

2 x 3 = six

Therefore, 6 is a multiple of both 2 and three. Therefore vi is said to exist a common multiple of both two and iii.

The To the lowest degree Common Multiple ( Fifty C Chiliad ) of two or more than numbers is divers every bit the smallest number ( other than zippo ) that is a multiple of those numbers. In other words, the least common multiple of two or more numbers is the smallest number which is divisible by all the given numbers. This ways that there cannot exist a number divisible past the given numbers and smaller than the to the lowest degree common multiple.

Permit u.s. understand this through an example.

Suppose nosotros accept two numbers, 8 and 12.

Let us check the multiples of these two numbers. We accept,

Multiples of 8 = eight, 16, 24, 32, 40 , 48, 56, 64, 72 and and so on…..

Multiples of 12 = 12, 24, 48, lx, 72 and so on …………

From above we tin run into that the common multipleS of 8 and 12 are 24, 48, 72 and and then on. Among these 24 is the least common multiple of these ii numbers. Therefore, 12 is the least common multiple or Fifty C Thou of eight and 12.

Nosotros accept merely seen that by writing the multiples of each number, we tin compare their multiples and observe out the least mutual multiple among them. Merely is this the just fashion to find the to the lowest degree common multiple or do we take some divers steps using which we can find the L C Grand of 2 or more numbers? Let us notice out.

How to Find a To the lowest degree Common Multiple ( L C Chiliad ) ?

There are ii major methods using which we can find the Fifty C M of ii or more than numbers. These methods are –

Prime Factorisation Method
Common Division Method

Let us discuss these methods one by one.

Prime Factorisation Method

As the proper noun suggests, the prime factorisation method involves finding the prime factors of the given numbers and and then computing the least common multiple ( L C M ). In this method, the following steps are used to find the L C M –

Obtain the given numbers.
Find the prime factors of each number.
Aggrandize each number equally a product of its prime factors
Find the production of all different prime factors with the highest power in the prime factorisation of each number.
The number obtained in the above step is the required L C M of the given numbers.

Let the states sympathize the above steps using an example.

Example

Notice the L C Thou of xl, 36 and 126 using the prime factorisation method.

Solution

We have been given the numbers 40, 36 and 126 and we are required to find the 50 C M of these numbers. Going by the above steps permit u.s.a. starting time detect the prime number factors of each of the given numbers. We have,

Prime factors of forty are –

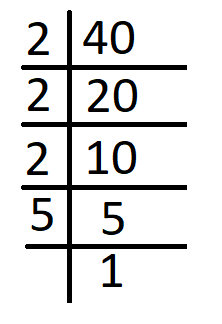
twoscore = two x two x 2 x v

Prime factors of 36 are –

36 = 2 x 2 ten three x 3

Prime number factors of 126 are –

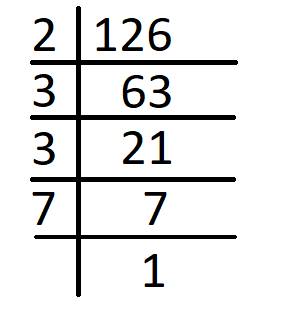
126 = 2 x 3 x three x 7

We can see in the above prime factorisations of the in a higher place numbers, the number 2 appears a maximum of three times, which is the instance in the number 40. Similarly, the number iii appears equally a gene for the maximum number of 2 times, which is the case in 36 and 126. The prime factors 5 and 7 occur only in xl and 126 respectively. Therefore, the required L C M of the numbers, twoscore, 36 and 126 will be

L C One thousand of twoscore, 36 and 126 = 2 x ii x 2 x 3 x 3 x v x seven = 2520

Hence, L C Yard of xl, 36 and 126 = 2520

Common Division Method

The following steps are followed to find the 50 C M of two or more than numbers using the mutual segmentation method –

Obtain the given numbers.
Conform the given numbers in a row separated by commas.
Obtain a number that divides exactly at to the lowest degree ii of the given numbers.
Split the numbers which are divisible by the number chosen in the above step and write the quotients merely beneath them. Carry forward the numbers which are not divisible.
Repeat the above steps till no ii of the given numbers are divisible by the same number.
Find the product of the divisors and the undivided numbers to get the required Fifty C M of the given numbers.

Allow us understand the higher up steps using an example.

Example

Find the L C M of 624 and 936 using the mutual division method.

Solution

Nosotros take been given the numbers 624 and 936 and nosotros are required to find the L C M using 624 and 936.

We have,

From the higher up common division we have,

Fifty C M of the numbers 624 and 936 = two x 2 x 2 x 3 x 13 x 2 ten 3 = 1872

Hence, 50 C M of the numbers 624 and 936 = 1872

Applications of Least Common Multiple ( L C M)

We shall now have a await at some applications of L C Yard in solving some practical problems. Let usa consider some examples.

Example 1 Determine the ii numbers nearest to 10000 which are exactly divisible by each of 2, 3, 4, 5, 6 and 7.

Solution The smallest number which is exactly divisible by 2, three, four, 5, 6 and 7 is their L C M. just, we have to find two numbers nearest to 10000 which are exactly divisible by the given numbers i.e. 2, 3, four, 5, 6 and 7. We tin can see that such numbers are multiples of the L C M of the given numbers. To find the L C M of ii, 3, 4, 5, 6 and 7 we have,

Therefore, the L C Thou of 2, 3, 4, 5, 6 and 7 is 420.

The number nearest to 10000 and exactly divisible by each of 2, iii, 4, 5, vi and 7 should also be exactly divisible by their L C Grand i.e. 420. Let u.s.a. now carve up 10000 by 420. We find that the residual is 340.

Number just less than 10000 and exactly divisible by 420

= 10000 – 340 = 9660.

Number just greater than 10000 and exactly divisible by 420

= 10000 + ( 420 – 340 ) = 10080

Hence the two numbers nearest to 10000 which are exactly divisible by each of 2, 3, 4, v, 6 and 79660 and 10080.

Example ii Sam has a photographic camera that allows 24 exposures whereas Peter has a camera that allows 36 exposures. Both of them want to be able to take the aforementioned number of photographs and complete their rolls of the picture. How many rolls should each buy?

Solution We take been given that Sam has a camera that allows 24 exposures whereas Peter has a photographic camera that allows 36 exposures. Both of them desire to exist able to have the aforementioned number of photographs and complete their rolls of the film.

Since the film in Sam'south photographic camera can take 24 exposures and the motion picture in Peter'southward camera tin take 36 exposures and both of them want to take the aforementioned number of photographs while completing the rolls of the film also, therefore, the total number of exposures taken by each will be the Fifty C Chiliad of 36 and 24. Hence, allow united states of america detect the L C M of 36 and 24.

We take,

From above, we can meet that the 50 C M of 36 and 24 = ii x two ten three x iii x ii = 72

Hence, the number of rolls Sam should buy will exist $\frac{72}{24}$ = 3

Similarly, the number of rolls Peter should buy will exist $\frac{72}{36}$ = 2

Fundamental Facts and Summary

A factor of a number is an exact divisor of that number.
A multiple of a whole number is the product of the number and whatsoever counting number.
If a number is a multiple of ii or more numbers, it is called a mutual multiple of the numbers.
Every multiple of a number is greater than or equal to that number.
The smallest multiple of a number is the number itself.
The number of multiples of a given number is infinite.
All multiples of 2 are even numbers.
Those multiples which are common among the multiples of 2 or more numbers are known every bit mutual multiples of those numbers.
We cannot define the largest multiple of a number or a group of numbers only we can e'er list out the first multiple of a number.
The Least Common Multiple ( L C M ) of two or more than numbers is divers equally the smallest number ( other than zero ) that is a multiple of those numbers.
There are 2 major methods using which we tin notice the Fifty C M of two or more numbers – Least Mutual Method ( L C Thousand ) and Common Division Method.
For finding the L C M using the Prime factorization method, nosotros expand each number equally a product of its prime factors. Then we find the product of all different prime factors with the highest ability in the prime factorisation of each number.
For finding the L C Grand using the mutual division method we split up the numbers which are divisible by the number chosen in the above step and write the quotients just below them. So nosotros carry forward the numbers which are not divisible.

Recommended Worksheets

Multiplying 1-Digit Whole Numbers by Multiples of x tertiary Grade Math Worksheets
Factors and Multiples (Ages 8-10) Worksheets (Space themed)
Understanding Factors and Multiples 4th Form Math Worksheets

Nosotros spend a lot of time researching and compiling the information on this site. If you find this useful in your inquiry, please use the tool below to properly link to or reference Helping with Math every bit the source. Nosotros appreciate your support!